Top strategies an algebra 2 tutor uses To teach rational equations effectively
Wiki Article
The Comprehensive Protection of Algebra 2 Tutoring: Secret Concepts and Abilities for Mastery
Algebra 2 tutoring supplies a broad spectrum of essential ideas and abilities essential for students to accomplish proficiency in mathematics. This encompasses a thorough understanding of polynomial functions, complex numbers, and logarithmic formulas, to name a few. Each subject improves the previous one, developing a natural structure for analytic. The application of these ideas in real-world circumstances highlights their relevance. There remain vital areas that can additionally boost a pupil's mathematical trip.Understanding Polynomial Functions
Just how do polynomial functions form the landscape of algebra? These fundamental expressions, containing variables raised to non-negative integer powers, work as the backbone of numerous algebraic ideas. They can be defined by their level, which shows the highest possible power of the variable, and their coefficients, which determine the function's actions. Polynomial features exhibit distinct residential or commercial properties, such as continuity and smoothness, permitting them to model a range of real-world situations. Their visual representations feature contours that can show various habits, including intercepts and turning factors. Comprehending polynomial functions involves understanding operations such as enhancement, multiplication, reduction, and department, in addition to factoring techniques. This fundamental understanding is necessary for resolving inequalities and formulas. By realizing polynomial functions, students create essential problem-solving abilities and get insight right into much more complex mathematical ideas, leading the way for sophisticated researches in algebra and past.Grasping Intricate Numbers

Interpretation and Residence
Complex numbers, a foundation of innovative algebra, prolong the concept of one-dimensional number lines to a two-dimensional airplane. Specified as numbers of the form (a + bi ), where (a) and (b) are actual numbers and (i) stands for the fictional unit with the property (i ^ 2 = -1 ), these numbers have unique homes. The actual part (a) indicates the straight axis, while the imaginary component (b) indicates the vertical axis in the facility aircraft. Secret residential or commercial properties include their capacity to stand for services to polynomial formulas that lack actual services and their closure under enhancement, division, subtraction, and reproduction (other than by zero) This framework permits for a deeper understanding of mathematical ideas and applications throughout various fields.Workflow With Facility Numbers
Procedures with intricate numbers form a crucial aspect of algebra that enhances mathematical understanding and analytical capabilities. Complicated numbers, shared in the form (a + bi), where (a) and (b) are real numbers, require details operations like addition, multiplication, reduction, and department.Enhancement and reduction entail incorporating like terms, while reproduction makes use of the distributive residential or commercial property and the reality that (i ^ 2 = -1) Division of intricate numbers demands increasing the numerator and by the conjugate to get rid of the imaginary part in the common denominator. algebra 2 help.
These operations not just enhance fundamental algebra skills but also prepare students for even more advanced topics, such as polynomial equations and square features. Mastery of complex number operations outfits students with vital logical devices.
Exploring Logarithmic Equations
In the research of logarithmic formulas, understanding the residential or commercial properties of logarithms is vital for effective analytic. These residential properties supply the foundational tools needed to adjust and simplify logarithmic expressions. By understanding these ideas, students can confidently tackle a selection of logarithmic equations.Recognizing Logarithm Features
Logarithm residential or commercial properties play a necessary function in streamlining and fixing logarithmic formulas, providing a methodical method to understanding their behavior. These residential properties consist of the power, quotient, and item rules. The item rule specifies that the logarithm of a product is the sum of the logarithms of its variables. On the other hand, the quotient guideline shows that the logarithm of a quotient is the difference of the logarithms. The power policy reveals that the logarithm of a number increased to a backer can be expressed as the exponent increased by the logarithm of the base. Proficiency of these buildings enhances one's capability to adjust logarithmic expressions, offering a structure for tackling much more complex equations and features experienced in innovative algebra.Solving Logarithmic Formulas
Exactly how can one effectively fix logarithmic formulas? To deal with these formulas, it is important to utilize properties of logarithms. One ought to settle logarithmic expressions using the item, quotient, and power policies. This simplification usually changes the formula right into a much more workable form. Next, converting logarithmic formulas to their rapid type can expose the unknown variable. For example, the formula (log_b(x) = y) converts to (x = b ^ y ) Additionally, examining options is important to assure they do not generate additional outcomes, particularly when taking care of logarithms. By methodically using these strategies, people can confidently browse and solve logarithmic equations, boosting their general understanding and proficiency of this mathematical idea.Examining Sequences and Collection
Sequences and collection may initially show up complicated, they are fundamental principles in algebra that expose patterns and connections within numbers. A series is a listing of numbers arranged in a details order, commonly defined by a formula or rule. Comprehending the types of series, such as arithmetic and geometric sequences, permits trainees to identify the underlying patterns successfully.On the other hand, a collection is the sum of the regards to a series. Examining collection includes recognizing limited and unlimited collection, in addition to computing their sums when applicable. Pupils learn vital strategies, such as More about the author using solutions for the amount of arithmetic and geometric series, which simplify calculations.
Grasping series and collection gears up students with necessary problem-solving skills, allowing them to tackle much more intricate mathematical concepts. This structure is crucial for their continued success in algebra and higher-level maths.
Solving Logical Expressions and Formulas
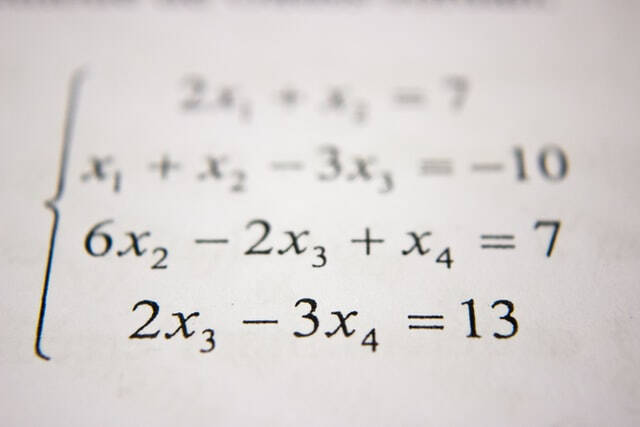
When addressing rational equations, one need to separate the variable, frequently by cross-multiplying to get rid of the portions. It is essential to check for supplementary remedies, as multiplying both sides can introduce values that do not satisfy the initial formula. Furthermore, pupils must be conscious of limitations on the variable, as specific worths can make the zero, rendering the expression undefined.
Comprehending Conic Sections
Conic sections are geometric figures obtained from the crossway of an airplane and a dual cone. These sections consist of circles, ellipses, parabolas, and hyperbolas, each distinguished by distinct properties and equations. Comprehending conic sections is important for trainees as they explore the relationships in between algebra and geometry.
Circles are specified by a consistent distance from a facility factor, while ellipses result from a plane reducing via both cones, creating a closed curve. Parabolas occur from a plane alongside the axis of the cone, showing a U-shaped chart. Hyperbolas, on the other hand, occur when the aircraft converges both halves of the cone, causing 2 distinct, open contours.
In Algebra 2, mastering conic sections involves acknowledging their standard equations, graphing them accurately, and identifying their essential functions, such as vertices, axes, and foci. This fundamental understanding prepares students for advanced mathematical principles.
Applying Charts and functions
Features and graphs act as fundamental devices in Algebra 2, allowing students to model relationships between variables and envision mathematical ideas. Proficiency of these elements permits learners to translate data, determine fads, and make predictions based upon established patterns. Trainees explore different kinds of functions, including straight, quadratic, polynomial, reasonable, and exponential, each with distinct attributes and applications.Graphing these features involves comprehending vital features such as intercepts, asymptotes, and inclines, which provide understandings right into their behavior. read Furthermore, pupils discover to transform features through reflections, stretches, and shifts, boosting their ability to manipulate and examine visual depictions.
Applying functions in real-world contexts even more strengthens understanding, as pupils take on troubles involving profit margins, population growth, and physics equations. This functional application bridges academic expertise with substantial end results, cultivating a much deeper admiration for the relevance of features and graphs additional reading in daily life.
Regularly Asked Questions
How Can I Improve My Problem-Solving Abilities in Algebra 2?
To enhance analytical abilities in Algebra 2, one must exercise frequently, look for varied problems, utilize on-line sources, team up with peers, and concentrate on understanding underlying ideas as opposed to memorizing procedures, cultivating much deeper understanding and application.What Resources Are Suggested for Additional Algebra 2 Technique?
Advised sources for extra Algebra 2 practice consist of online systems like Khan Academy, textbooks with practice problems, and tutoring solutions. Involving in math forums can also give varied analytical techniques and joint understanding possibilities.Are There Online Tutoring Options Available for Algebra 2?
Yes, various on the internet tutoring options exist for Algebra 2 (algebra 2 tutoring). Systems like Khan Academy, Chegg Tutors, and Wyzant offer personalized aid, video clip lessons, and interactive exercises, accommodating numerous discovering styles and timetables for trainees seeking assistanceExactly how Do I Get ready for Algebra 2 Exams Properly?
To prepare effectively for Algebra 2 tests, one ought to assess essential principles, method troubles on a regular basis, utilize on-line resources, develop study hall, and take practice examinations to identify staminas and bents targeted enhancement.
What Are Usual Mistaken Beliefs Students Have in Algebra 2?
Pupils usually misinterpret the significance of foundational principles, thinking they can skip requirements. They might likewise have problem with abstract reasoning, puzzling functions with formulas, and misinterpreting the role of variables in algebraic expressions.Understanding complex numbers is essential for pupils in Algebra 2, as these numbers prolong the real number system to fix equations that do not have genuine solutions. These procedures not just strengthen foundational algebra abilities but additionally prepare students for more innovative topics, such as polynomial formulas and square functions. Reasonable expressions and formulas represent crucial parts of algebra, involving fractions where the numerator and are polynomials. In Algebra 2, understanding conic sections includes acknowledging their basic formulas, graphing them properly, and identifying their crucial functions, such as axes, foci, and vertices. Applying features in real-world contexts further solidifies comprehension, as trainees take on troubles involving profit margins, population growth, and physics formulas.
Report this wiki page